This post is part of our Guide to Bayesian Statistics

Food allergies are a big deal. Nearly everyone has had to accommodate someone with a food allergy. Sometimes it's switching from making your kid Peanut Butter and Jelly to Sunflower Butter and Jelly, making a gluten-free appetizer for a party, or cooking a separate meal for a guest. While most people try their best to be considerate, I think everyone without a food allergy, myself included, has wondered "but do they really have a food allergy?". Even the Boston Globe published an article, back in October, "Why food allergy fakers need to stop". The value of probability theory is that we can quantify our skepticism and make rational choices from this analysis. In this post we're going to answer the question "How Skeptical Should I be if my friend claims to have a Food Allergy"?

The Data

Thankfully the Boston Globe article points to a paper from 2003 that gives us some data to work with. The essential things we'd like to know for our analysis are: how many people truly have a food allergy and how many people claim to have a food allergy (independent of whether or not they have one). We'll denote "has an allergy" with a variable $A$. One crucial thing to note is that there is a notable difference between children and adults. The analysis is going to be different depending on whether you're desperately searching the grocery store non-nut butter at 10 pm because your kid needs a sandwich in the morning, or searching for a gluten-free restaurant for a night out with friends.

The article gives the probability of a food allergy in children as being between 4%-8% and for adults 1%-2%. For our analysis, we'll assume the middle values, but keep in mind that we could be more conservative in our estimates. Now we can write these down as two probabilities:

$$P(A_{\text{child}})=0.06$$
$$P(A_{\text{adult}})=0.015$$

The only other piece of data we need is the probability that someone will claim they have a food allergy. We'll use the variable $C$ for "claims they have an allergy" (or that their kids do). Luckily the article states that both adults and parents of children claim that either they or their children have a food allergy 30% of the time. For the probability that someone will claim they or their child has a food allergy we get:

$$P(C) = 0.3$$

The article says "up to 30%", so it's important to realize that this is an upper bound. It is critical to keep in mind when we do our analysis that we're choosing the mean value for how likely a person is to have an allergy and a more extreme value for estimating how likely the are to claim they have an allergy. Because of these choices our analysis is going to be biased in favor of the claim that they are "faking it". We're stuck with this since the article doesn't give us more info on the 30% figure.

The Analysis

The question we want to answer is: Given someone claims a food allergy, what is the probability that they truly do have an allergy?

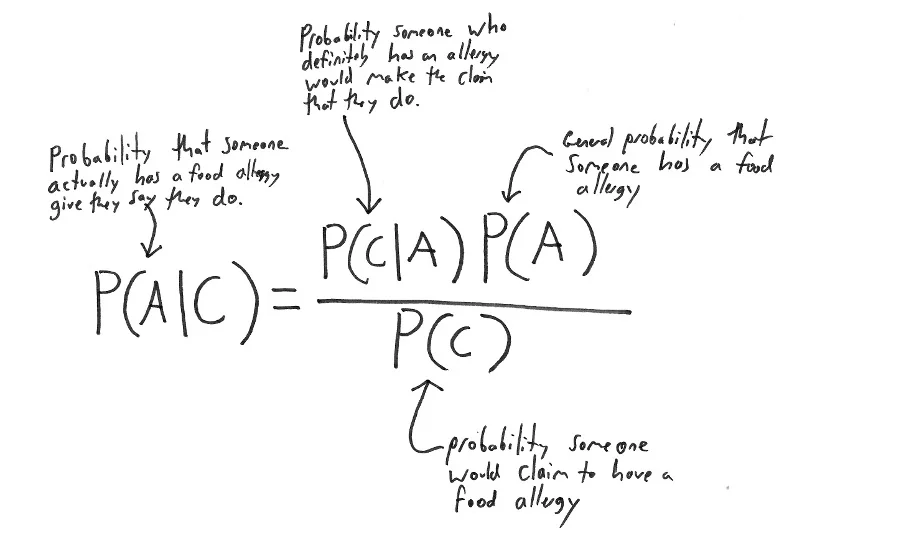
In math we would express this as "What is the probability of $A$ given $C$" and in a formula:

$$P(A|C)$$

Given that we know both $P(A)$ and $P(C)$ we can use Bayes' Theorem!

$$P(A|C) = \frac{P(C|A)\cdot P(A)}{P(C)}$$

Let's break this down so our reasoning is clear:

What all the terms in Bayes' Theorem mean for our example

We know both $P(A)$ for both adults and children and $P(C)$. The only thing we don't know explicitly is $P(C|A)$, but I'm going to assume that if you do have a food allergy, then there is a 100% chance you will claim to have one.
$$P(C|A) = 1$$

All we have to do is plug in our values and see what our results are:

$$P(A_{\text{child}}|C)= \frac{P(C|A)\cdot P(A_{\text{child}})}{P(C)} = \frac{1\cdot 0.06}{0.3} = 20\%$$

$$P(A_{\text{adult}}|C)= \frac{P(C|A)\cdot P(A_{\text{adult}})}{P(C)} = \frac{1\cdot 0.015}{0.3} = 5\%$$

Given the data we have, if a parent claims their child has a food allergy there's a 20% chance that child truly does and if your friend claims they have a food allergy there's only a 5% chance.

So your friends are liars, right?

Now is the time when it is most important to think like Probabilists. The naive approach to these results is "see! They're all lying!".We find that there is an 80% chance that a parent is wrong about their children, and a friend has a 95% chance of "faking" (this is a dangerous assumption) that gluten allergy they talk about. That looks pretty damning.

If you have read the post on the different between being 90% and 99% certain, then you'll remember that there is an enormous difference between being 95% certain and 99% certain of something. The difference is nearly an order magnitude! For the case of children being 80% certain is roughly the same as getting a p-value of 0.2, which even the most sketchy academic journal would throw out as being meaningless.

What about the adults with 95% certainty they are "faking"? When people ask me for advice about running A/B tests I always recommend they run the tests until they are at least 99% certain of their results. If I wouldn't call an A/B test at 95% certainty, I would certainly not call my friend a liar at 95% certainty. Furthermore, as discussed earlier, our analysis is biased for the "faking it" hypothesis.

The cost of being wrong

Being certain isn't everything either. What's the risk of going with the wrong variant in an A/B test? A few lost customers until the next round of testing, likely a small fraction of your overall revenue in the long run. The risk of being wrong with a friend's food allergies is far, far more dangerous. If you said "I'm 95% certain this is rocket is good to launch" you would never fire that rocket! Even if you were 99.9% certain that everything was good, that would still be way too much uncertainty for something as catastrophic as the failure of a rocket to launch. In the case of children, being 80% certainty is basically saying "I have no idea". This low level of belief is not worth risking a tummy ache let alone threatening a life. For your friend, being 95% certain is nowhere near certain enough to not put in the effort to find a restaurant with a gluten-free menu.

Conclusion

While the data technically claims that friends are "more likely than not" to be wrong about their food allergy, "more likely than not" doesn't mean all that much in probability. To form strong beliefs we want our data to show something is dramatically more likely than not to be true. More importantly, we must always weigh our certainty with the risk. If you are betting a dollar, a 55% chance that a game is in your favor might be a smart bet. If you are betting your house, being 99% certain is likely not enough. From the view of probability, it is sage advice to trust people when claim to have an allergy.

If you enjoyed this post please subscribe to keep up to date and follow @willkurt!